第一章 引论

电压传输特性

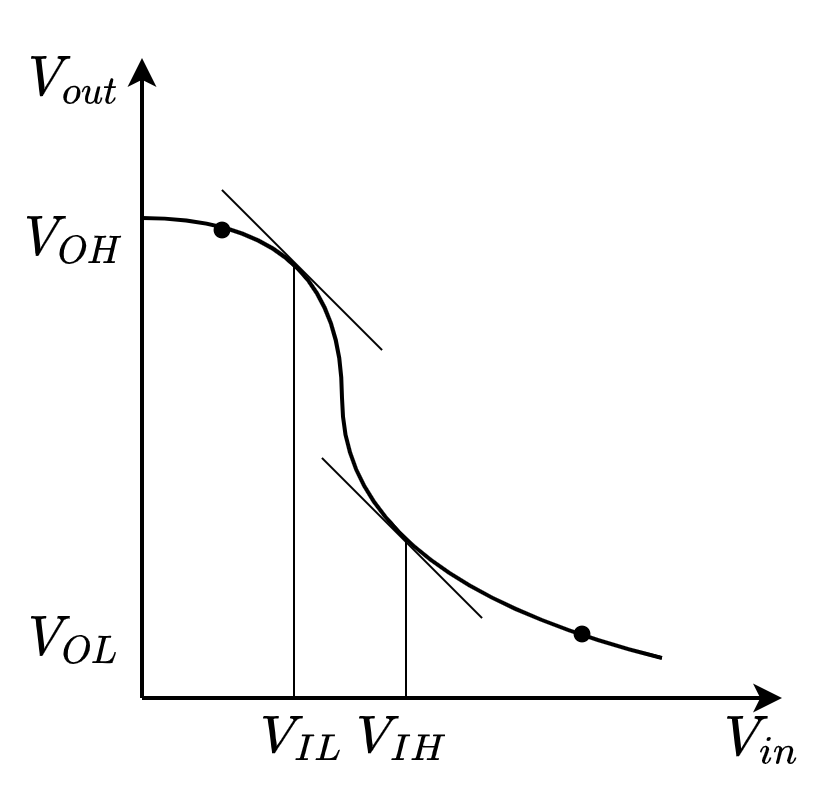
现在假设一个反相门电路的输入为逻辑变量 in，它产生输出变量 out。一个逻辑门的电路功能可以用它的电压传输特性（VTC，有时称为 DC 传输特性）得到最佳描述，它画出了输出电压与输入电压的关系 $V_{out}=f\left(V_{in}\right)$

• 额定高电压 $V_{OH}$ 和额定低电压 $V_{OL}$ $$V_{OH}=f\left(V_{O L}\right),V_{O L}=f\left(V_{O H}\right)$$
• 门阈值电压或开关阈值电压 $V_{M}$ $$V_{M}=f\left(V_{M}\right)$$
• VTC 增益 $$gain = \frac{\mathrm{d} V_{out}}{\mathrm{d} V_{in}}$$
• 可接受的高电压 $V_{IH}$ 和低电压 $V_{IL}$ 代表了 VTC 增益等于 -1 的点

噪声容限

一个门对噪声的灵敏度是由低电平噪声容限 $N M_{L}$ 和高电平噪声容限 $N M_{H}$ 来度量的。它们分别量化了合法的“0”和“1”的范围，并确定了噪声的最大固定阈值：

$$\begin{array}{c} N M_{L}=V_{I L}-V_{O L} \\ N M_{H}=V_{O H}-V_{I H} \end{array}$$

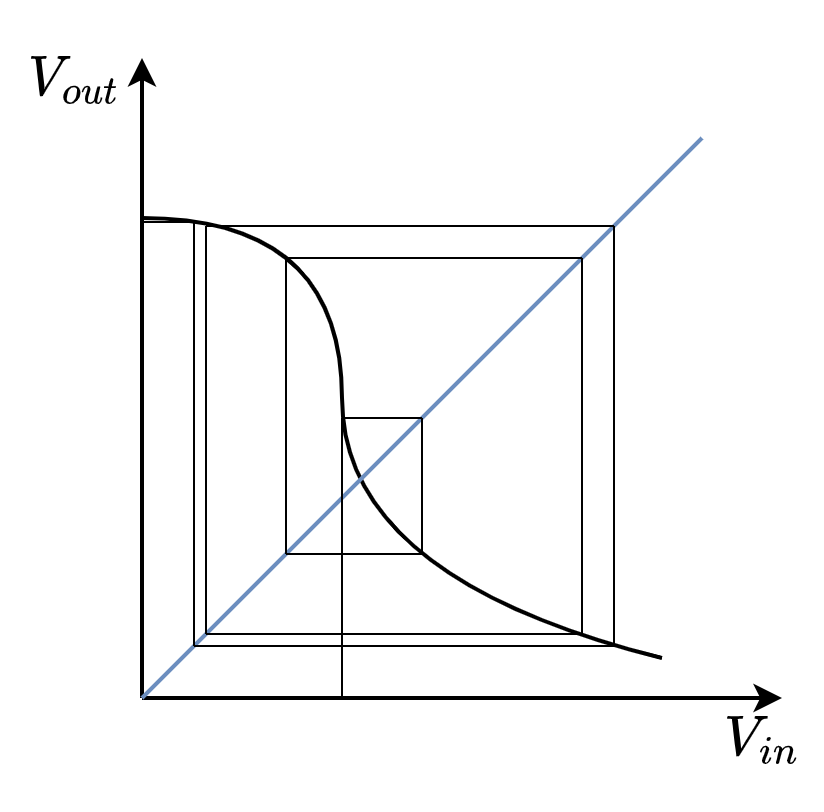
再生性

再生性保证一个受干扰的信号在通过若干逻辑级后逐渐收敛回到额定电平中的一个。

抗噪声能力

（Todo）

扇入和扇出

• 扇出表示连接到驱动门输出端的负载门的数目 N。
  • 增加一个门的扇出会影响它的逻辑输出电平。通过使负载门的输入电阻尽可能地大（也就是使输入电流最小）并保持驱动门的输出电阻较小（即减小负载电流对输出电压的影响），可以使这一影响减到最小。
  • 当扇出较大时，所加的负载会使驱动门的动态性能变差。为此许多通用单元和库单元都定义了一个最大扇出数来保证该单元的静态和动态性能都能满足规定的技术要求。
• 扇入定义为该门输入的数目。扇入较大的门往往比较复杂，这常常会使静态和动态特性变差。

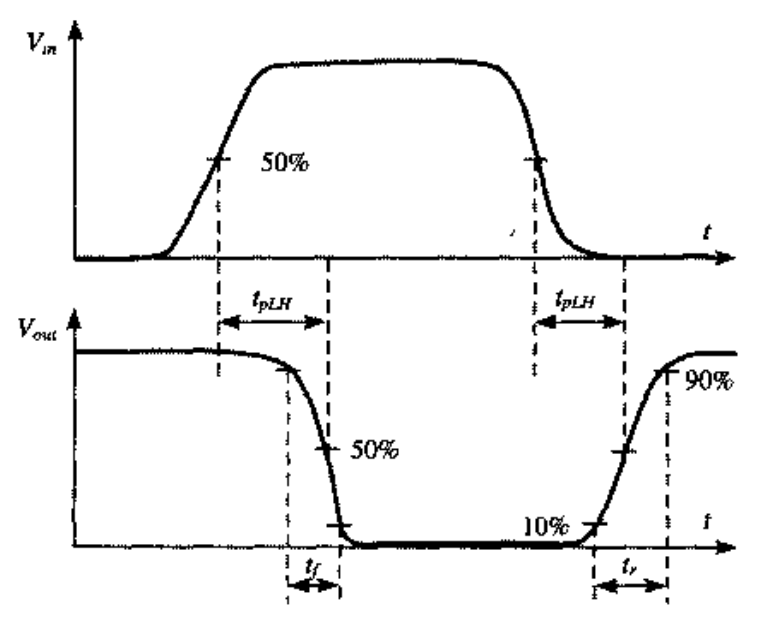
传播延时

一个门的传播延时 $t_{p}$ 定义了它对输入端信号变化的响应有多快。它表示一个信号通过一个门时所经历的延时，定义为输入和输出波形的 $50\%$ 翻转点之间的时间。由于一个门对上升和下降输入波形的响应时间不同，所以需要定义两个传播延时。$t_{p L H}$ 定义为这个门的输出由低至高（或正向）翻转的响应时问，而 $t_{p H L}$ 则为输出由高至低（或负向）翻转的响应时间。传播延时 $t_{p}$ 定义为这两个时间的平均值：

$$t_{p}=\frac{t_{p L H}+t_{p H L}}{2}$$

对于 RC 电路

• 充电：$V_{out}(t)=V_{dd}(1-e^{-t/\tau})$
• 放电：$V_{out}(t)=V_{dd}e^{-t/\tau}$

功耗与能耗

• 功耗可以进一步划分成静态部分和动态部分。
  • 动态功耗只发生在门开关的瞬间。这是由于对电容充电以及在电源和地之间有一暂时的电流通路造成的，因此它正比于开关频率
  • 静态功耗即使在没有发生开关时也存在，并且是由在电源和地之间的静态导电通路或由于漏电流引起的
• 一个门的传播延时和功耗有关，能量的传送越快（或者说功耗越大）则门越快。
  • 对于给定的工艺和门的拓扑结构,功耗和延时的乘积一般为一常数。这一乘积称为功耗-延时积（PDP），它可以作为一个开关器件质量的度量。
• 一个理想的门应当快速且几乎不消耗能量，能量-延时积（E-D）是把这两个因素放在一起考虑的复合标准，它经常作为最后的质量评价。

第二章 制造工艺

（Todo）

第三章 器件

MOSFET 电容模型

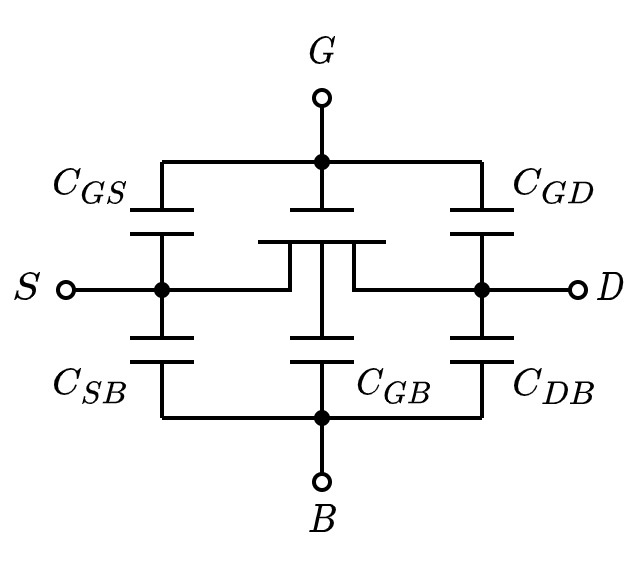
• 覆盖电容 $C_{overlap}=C_{GSO}+C_{GDO}$
• 栅至沟道的电容 $C_{GC}=C_{GCB}+C_{GCS}+C_{GCD}$

• 扩散电容 $C_{diff}=C_{Sdiff}+C_{Ddiff}$

• $C_{GS}=C_{GSO}+C_{GCS}$

• $C_{GD}=C_{GDO}+C_{GCD}$
• $C_{GB}=C_{GCB}$
• $C_{SB}=C_{Sdiff}$

• $C_{DB}=C_{Ddiff}$

• $C_{G}=C_{GC}+C_{overlap}$

术语介绍

英文名	中文名	解释
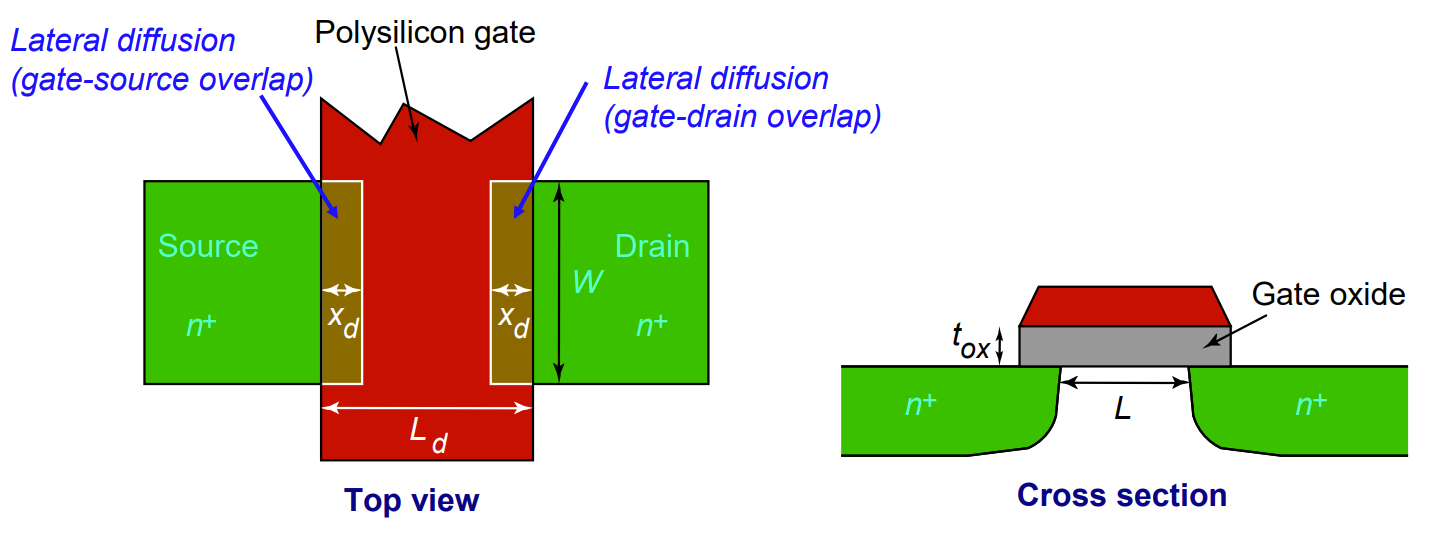
Overlap cap	覆盖电容	源和漏在氧化层下延展的横向扩散引起的栅和源漏间的寄生电容
Channel capacitances	沟道电容	栅至沟道的电容，包含栅至源、栅至漏、栅至体的电容，是MOS最重要的寄生电路部分
Junction/diffusion capacitances	结电容/扩散电容	反向偏置的源体、漏体间的pn结引起的电容
Bottom-plate cap	底板电容	扩散区底板的pn结电容，由源/漏（掺杂为 $N_{D}$）和衬底（掺杂为 $N_{A}$）形成
Side-well cap	侧壁电容	扩散区侧壁的pn结电容，由源/漏（掺杂为 $N_{D}$）和掺杂为浓度为$N_{A}^{+}$ 的 $p+$ 沟道阻挡层注入形成

覆盖电容

$$C_{GSO}=C_{GDO}=C_{ox}x_{d}W$$

栅电容

$$\begin{array}{|c|c|c|c|c|c|} \hline \text { 工作区 } & C_{G C B} & C_{G C S} & C_{G C D} & C_{G C}=C_{G C B}+C_{G C S}+C_{G C D} & C_{G}=C_{G C}+C_{\text {overlap }} \\ \hline \text { 截止 } & C_{o x} W L & 0 & 0 & C_{o x} W L & C_{o x} W L+2 C_{o} W \\ \hline \text { 线性 } & 0 & C_{o x} W L / 2 & C_{o x} W L / 2 & C_{o x} W L & C_{o x} W L+2 C_{o} W \\ \hline \text { 饱和 } & 0 & (2 / 3) C_{o x} W L & 0 & (2 / 3) C_{o x} W L & (2 / 3) C_{o x} W L+2 C_{o} W \\ \hline \end{array}$$

扩散电容

$$C_{SB}=C_{Sdiff}=AS*C_{jbs}+PS*C_{jbssw}+W*C_{jbsswg}$$ $$\begin{array}{l} A S=L_{S} * W \\ P S=\left(2 L_{S}+W\right)+W \\ C_{j b s}=C_{J}\left(1+\frac{V_{S b}}{\psi_{0}}\right)^{-M_{J}} \\ C_{j b s s w}=C_{J S W}\left(1+\frac{V_{S b}}{\psi_{0}}\right)^{-M_{J S W}} \\ C_{j b s s wg}=C_{J S W}\left(1+\frac{V_{S b}}{\psi_{0}}\right)^{-M_{J S WG}} \\ \psi_{0}=\frac{k T}{q} \ln \left(\frac{N_{D} N_{A}}{n_{i}^{2}}\right) \end{array}$$

其中

• $C_{SB}$ 是源区结电容
• $C_{jbs}$ 是单元区域衬底至源区底部结电容
• $C_{J}$ 是单元区域零偏压电容
• $C_{jbssw}$ 是单位周长衬底至源区侧壁结电容
• $C_{JSW}$ 是单位周长零偏压侧壁结电容
• $C_{jbsswg}$ 是单位周长衬底至源区栅边侧壁结电容
• $C_{JSWG}$ 是单位周长零偏压栅边侧壁结电容
• $AS$ 是源区底部面积
• $PS$ 是源区侧壁周长
• $\Phi_0$ 是内建电势
• $V_{sb}$ 是源和衬底间的电势
• $M_{J},M_{JSW},M_{JSWG}$ 是结缓变系数

阈值压降

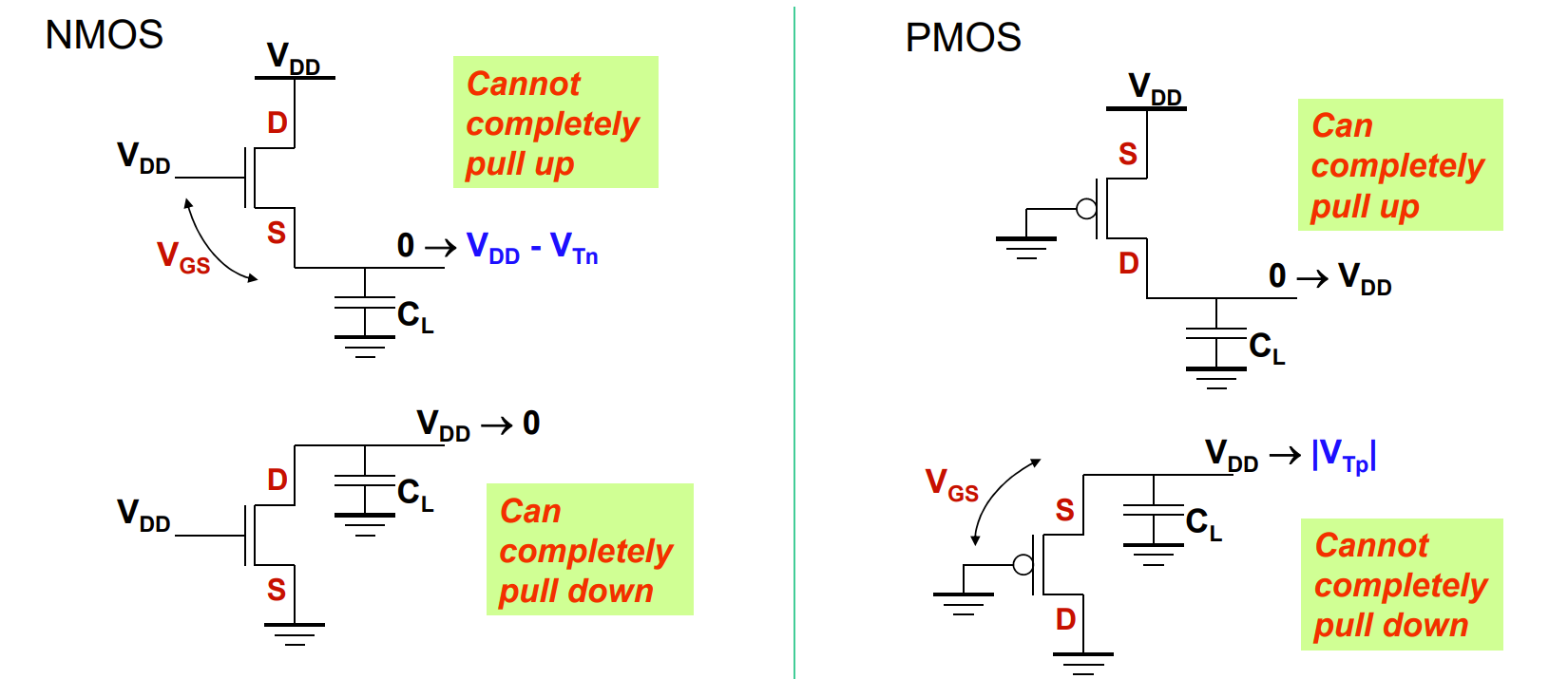
• NMOS Transistors pass a “strong” 0 but a “weak” 1
• PMOS Transistors pass a “strong” 1 but a “weak” 0
• NMOS 不能被完全上拉，可以被完全下拉
• PMOS 不能被完全下拉，可以被完全上拉

体偏效应

$$V_{T}=V_{T 0}+\gamma\left(\sqrt{\left|-2 \phi_{F}+V_{S B}\right|}-\sqrt{\left|2 \phi_{F}\right|}\right)$$

其中体效应系数

$$\begin{array}{c} \gamma_{N M O S}=\frac{t_{o x}}{\varepsilon_{O x}} \sqrt{2 q \varepsilon_{S i} N_{A}}=\frac{\sqrt{2 q \varepsilon_{S i} N_{A}}}{C_{O x}} \\ \gamma_{P M O S}=-\frac{t_{O x}}{\varepsilon_{O x}} \sqrt{2 q \varepsilon_{S i} N_{D}}=-\frac{\sqrt{2 q \varepsilon_{S i} N_{D}}}{C_{O x}} \\ \end{array}$$

费米电势

$$\begin{array}{c} \phi_{F_{-} N M O S}=\frac{k T}{q} \ln \frac{n_{i}}{N_{A}} \\ \phi_{F_{-} P M O S}=\frac{k T}{q} \ln \frac{N_{D}}{n_{i}} \end{array}$$

• 对于NMOS
  • 正体偏，$V_{BS}>0$，$V_T$ 减小
  • 负体偏，$V_{BS}<0$，$V_T$ 增大
• 对于PMOS
  • 正体偏，$V_{BS}>0$，$V_T$ 增大
  • 负体偏，$V_{BS}<0$，$V_T$ 减小

第五章 反相器

人工分析的统一模型

$$\begin{array}{l} I_{D}=0 \text { for } V_{G T} \leq 0 \\ I_{D}=k^{\prime} \frac{W}{L}\left(V_{G T} V_{\text {min }}-\frac{V_{m i n}^{2}}{2}\right)\left(1+\lambda V_{D S}\right) \text { for } V_{G T} \geq 0 \\ \text { with } V_{\text {min }}=\min \left(V_{G T}, V_{D S}, V_{D S A T}\right), \\ V_{G T}=V_{G S}-V_{T}, \\ \text { and } V_{T}=V_{T 0}+\gamma\left(\sqrt{\left|-2 \phi_{F}+V_{S B}\right|}-\sqrt{\left|-2 \phi_{F}\right|}\right) \end{array}$$

类型	$V_{T0}$	$\gamma$	$V_{Dsat}$	$k’$	$\lambda$
NMOS	0.43	0.4	0.63	115e-6	0.06
NMOS	-0.4	-0.4	-1	-30e-6	-0.1

静态CMOS反相器特性

• 输出高电平和低电平分别为 $V_{dd}$ 和 $GND$。换言之，电压摆幅等于电源电压。因此噪声容限很大。
• 逻辑电平与器件的相对尺寸无关，所以晶体管可以采用最小尺寸。具有这一特点的门称为无比逻辑。它不同于有比逻辑，在有比逻辑中逻辑电平是由组成逻辑的晶体管的相对尺寸来决定的。
• 稳态时在输出和 $V_{dd}$ 或 $GND$ 之间总存在一条具有有限电阻的通路。因此一个设计良好的 CMOS 反相器具有低输出阻抗，这使它对噪声和干扰不敏感。输出电阻的典型值在 $k\Omega$ 的范围内。
• CMOS反相器的输入电阻极高，因为一个MOS管的栅实际上是-个完全的绝缘体，因此不取任何dc（直流）输入电流。由于反相器的输入节点只连到晶体管的栅上，所以稳态输入电流几乎为零。
• 理论上，单个反相器可以驱动无穷多个门（或者说具有无穷大的扇出）而仍能正确工作，但我们很快会看到增加扇出也会增加传播延时。尽管扇出不会对稳态特性有任何影响，但它使瞬态响应变差。
• 在稳态工作情况下电源线和地线之间没有直接的通路（即此时输入和输出保持不变）。没有电流存在（忽略漏电流）意味着该门并不消耗任何静态功率。

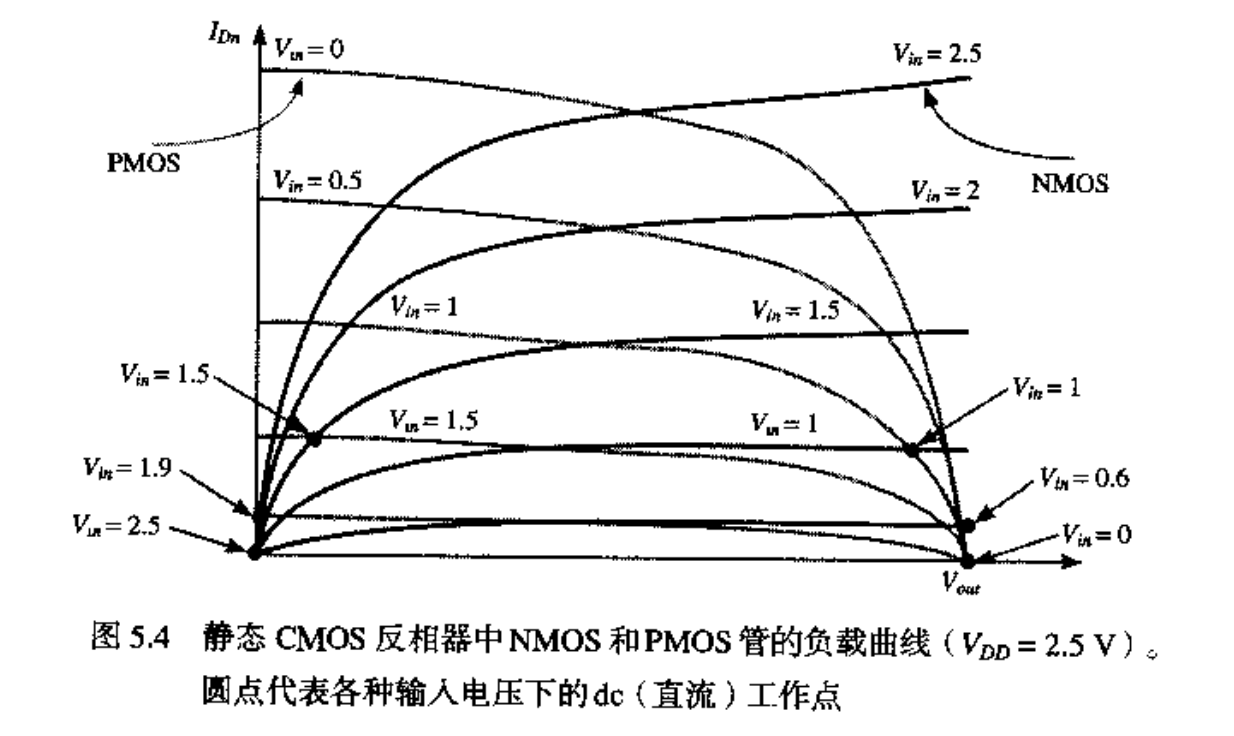
VTC（电压传输特性）

电压传输特性（VTC）的性质和形状可以通过图解法迭加 $NMOS$ 和 $PMOS$ 器件的电流特性来得到。这样的一个图形结构通常称为负载曲线图。它要求把 $NMOS$ 和 $PMOS$ 器件的 $I-V$ 曲线转换到一组公共坐标上。我们以输入电压 $V_{i \pi}$、输出电压 $V_{\mathrm{out}}$ 和 $NMOS$ 漏电流 $I_{D N}$ 作为选择的变量，于是 $PMOS$ 的 $I-V$ 关系就可以通过以下关系转换到这一变量空间中（下标 $n$ 和 $p$ 分别表示 $NMOS$ 和 $PMOS$ 器件）：

$$\begin{array}{c} I_{D S p}=-I_{D S n} \\ V_{G S n}=V_{i n} \quad V_{G S p}=V_{i n}-V_{D D} \\ V_{D S n}=V_{O u t} \quad V_{D S p}=V_{o u t}-V_{D D} \end{array}$$

理想CMOS反相器的VTC：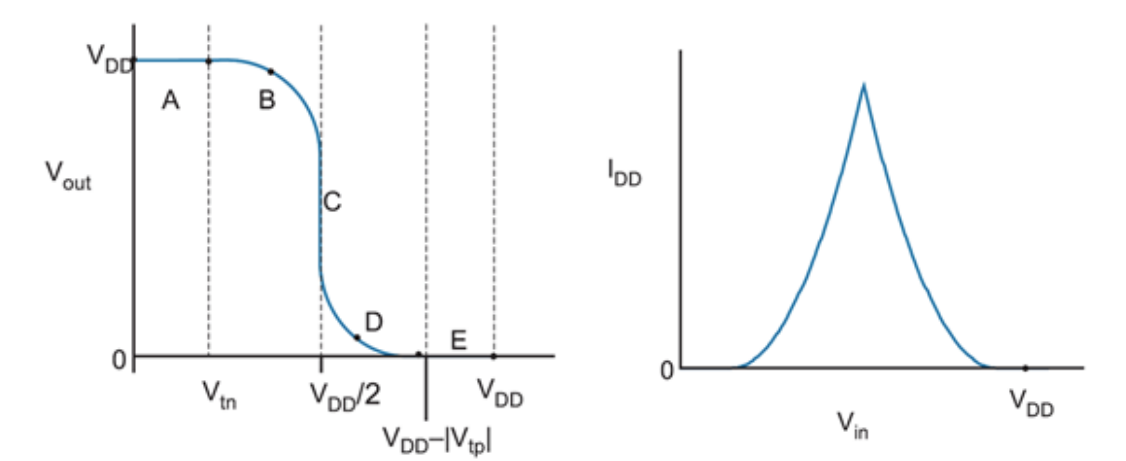

区域	条件	PMOS	NMOS	输出
A	$[0,V_{Tn}]$	线性	截止	$V_{DD}$
B	$[V_{Tn},V_{DD}/2]$	线性	饱和	$>V_{DD}/2$
C	$V_{DD}/2$	饱和	饱和	$X$
D	$[V_{DD}/2,V_{DD}-\mid V_{Tp}\mid]$	饱和	线性	$<V_{DD}/2$
E	$[V_{DD}-\mid V_{Tp}\mid,V_{DD}]$	截止	线性	$0$

阈值电压

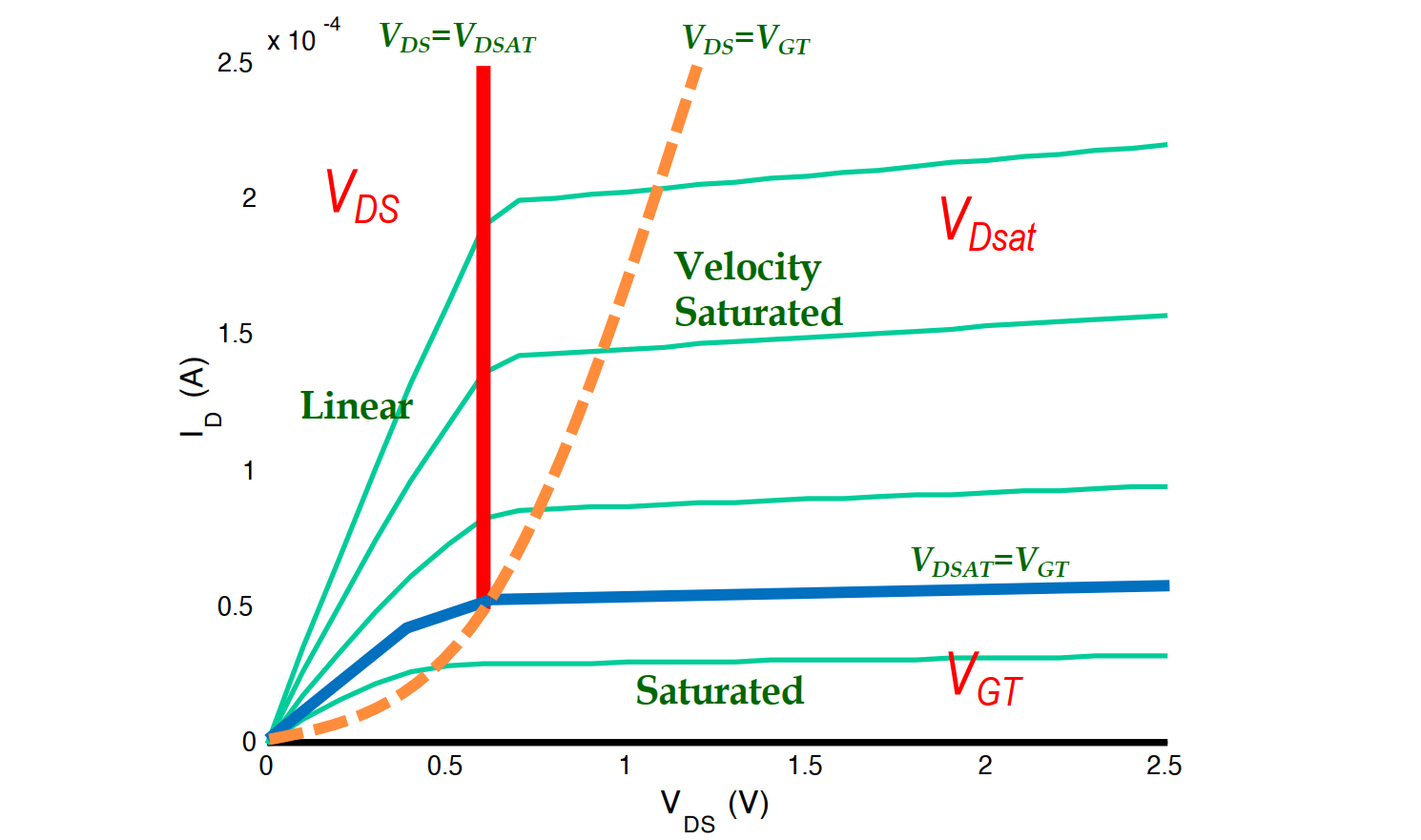
开关阈值 $V_{M}$ 定义为 $V_{in}=V_{out}$ 的点，其值可以用图解法由 VTC 与直线 $V_{in}=V_{out}$ 的交点求得。在这一区域由于 $V_{DS}=V_{GS}$，PMOS 和 NMOS 总是饱和的。使通过两个晶体管的电流相等就可以得到 $V_{M}$ 的解析表达式。我们求解的情形是电源电压足够高，所以这两个器件可以被假设为都处于速度饱和（即 $V_{D S A T}<V_{M}-V_{T}$）。同时我们忽略沟长调制效应，于是有：

$$k_{n} V_{D S A T n}\left(V_{M}-V_{T n}-\frac{V_{D S A T n}}{2}\right)+k_{p} V_{D S A T P}\left(V_{M}-V_{D D}-V_{T p}-\frac{V_{D S A T p}}{2}\right)=0$$

求解 $V_{M}$ 得到：

$$V_{M}=\frac{\left(V_{T n}+\frac{V_{D S A T n}}{2}\right)+\gamma\left(V_{D D}+V_{T p}+\frac{V_{D S A T p}}{2}\right)}{1+\gamma}$$

其中

$$\gamma=\frac{k_p V_{Dsat_p}}{k_n V_{Dsat_n}}=\frac{k_p^{\prime} V_{Dsat_p}}{k_n^{\prime} V_{Dsat_n}}N$$

• 为了让 $V_{M}$ 接近 $V_{DD}$，$\gamma$ 应该在 3~4 之间

增益

$$\begin{aligned} g & =\left.\frac{\mathrm{d} V_{out}}{\mathrm{d} V_{in}}\right|_{V_{in}=V_{M}} \\ & =-\frac{1}{I_{D}\left(V_{M}\right)} \frac{k_{n} V_{DSATn}\left(1+\lambda_{n} V_{out}\right)+k_{p} V_{DSATp}\left(1+\lambda_{p} V_{out}-\lambda_{p} V_{D D}\right)}{\left(\lambda_{n}-\lambda_{p}\right)} \\ & \approx-\frac{1+\gamma}{\left(V_{M}-V_{T n}-V_{D S A T n} / 2\right)\left(\lambda_{n}-\lambda_{p}\right)} \end{aligned}$$

若

• 尺寸比增大
• $V_{DD}$ 减小

则增益增大

噪声容限

$$\begin{array}{l} V_{I H}=V_{M}-\frac{V_{M}}{g}\\ V_{I L}=V_{M}+\frac{V_{D D}-V_{M}}{g} \\ N M_{H}=V_{D D}-V_{I H}\\ N M_{L}=V_{I L} \end{array}$$

注意 $g$ 是负数